With a small correction in the market, I, Diego García del Río, I believe that this is the right time to implement one of my strategies. Remember that none of what I am saying constitutes investment advice, I am simply sharing my activity and dynamics within the financial market.
As I mentioned, after the liquidation of a part of positions, already notified by my market forum and social networks, I started this strategy.
The typical structure is based on delta 50 ATM contracts, used as a hedging mechanism to hedge against a possible market correctionespecially in indexed and leveraged ETFs.
On this occasion with the small correction occurredthis time I will carry out this strategy in OTMspecifically between a 8-10% of the underlying price.
My chosen position is: $SPXL STK 220 VTO JAN16'26
The main objective of this strategy is to maintain exposure to the market in the event of a upside moderate, while avoiding excessive exposure to a correction. In this way, the risk is limited to the loss of the premium, while insuring the remaining upside performance until the correction I foresee, with the intention of reopen exposure in my futures strategy once the correction is made.
How this Hedging Strategy Works
The basic operation consists, with no exceptions such as this time, of maintaining contracts around delta 50renewing the position when current contracts are close to the end of the year. 45 days to maturity (DTE)The objective is to avoid the phase of the highest temporary depreciation (theta decay). In this way, the strategy seeks to capture a potential return of close to 100% per cyclewhile at the same time preserving that remaining upside exposure and offering flexibility to roll the position according to market developments.
I, Diego García del Río, carry out this strategy on the following topics ETFs linked to benchmark indices such as the SPX and the NDXalso Leveraged ETFs such as SPXL and TECLThis allows us to replicate the performance of the main equity markets with a systematic risk management framework.
On this occasion, which I will notify through my market forum and social networks, I will be looking for long maturity contracts, I propose contracts at the beginning of 2027.
Example Hedging Strategy Basis
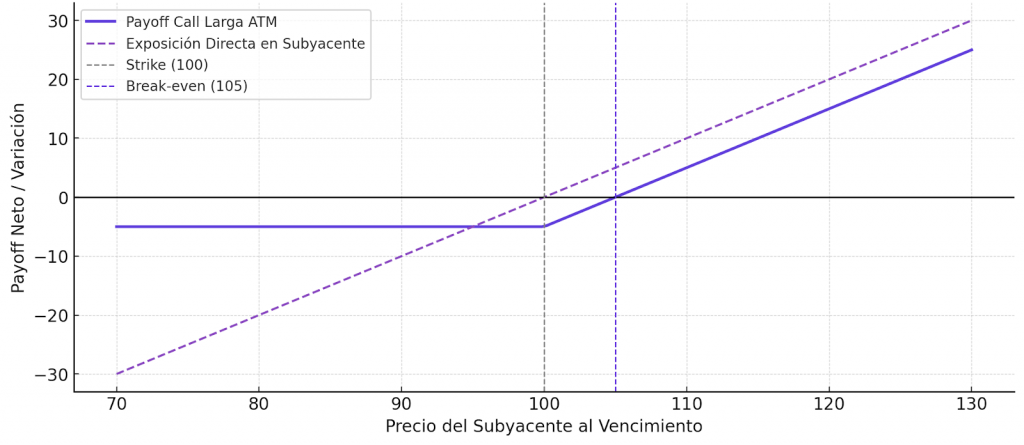
As an illustrative example of this strategy, one long call ATM with strike at 100 and a premium paid of 5 has a clear and asymmetric payoff profile. The maximum loss is limited to the paid-in premium (-5), regardless of what happens to the underlying on the downside. This implies that for expiration prices at 70, 80, 90, 95 or even 100, the intrinsic value of the option is nil and the net result remains at -5, equivalent to a -100% of return on premium.
| Price at Maturity | Intrinsic Value | Net Payoff | ROI on Premium |
| 70 | 0 | -5 | -100% |
| 80 | 0 | -5 | -100% |
| 90 | 0 | -5 | -100% |
| 95 | 0 | -5 | -100% |
| 100 | 0 | -5 | -100% |
| 105 | 5 | 0 | 0% (break-even) |
| 110 | 10 | +5 | +100% |
| 115 | 15 | +10 | +200% |
| 120 | 20 | +15 | +300% |
| 125 | 25 | +20 | +400% |
| 130 | 30 | +25 | +500% |
The point of break-even is set at 105, the level at which the intrinsic value exactly offsets the premium paid. Above this threshold, convexity amplifies the relative return:
- At 110, the net payoff amounted to +5 (+100% ROI).
- At 120, net income grew to +15 (+300%).
- At 130, it reaches +25 (+500%).
To better understand the difference versus a direct equity exposure, let's assume the purchase of 100 shares of the same underlying at 100 each. On a drop to 95, 90, 80 or 70, the loss would be -500, -1000, -2000 and -3000 respectively, with no defined limit beyond the zero price.
With the use of options, the risk is limited: purchasing a call contract (representing 100 shares) for a premium of 5 implies a total cost of 500. The maximum loss will be that amount, even if the underlying were to fall to zero.
In this way, the options make it possible to define and control risk from the outset, while preserving the unlimited upside potential.
Characteristics of the Hedging Strategy
Selection of ATM delta 50 contracts
The following are used calls at-the-money (ATM)Although, as I say, there may be exceptional cases, since I see a higher upside in strikes below delta 50, likewise, it is usually delta 50 to maximize exposure to the movement of the underlying. In this area, the gamma is higherThis means that small variations in the price generate larger proportional changes in the delta, amplifying the sensitivity of the option. This greater convexity The new system allows for more efficient capture of the underlying's shifts, while maintaining a natural symmetry between the risk assumed and the probability of the option ending in the money.
Time horizon and theta management
Positions are maintained as long as they exceed 45 days to maturity. In this range, time erosion is more moderate and the premium value remains more stable. Above this threshold, the theta-decay accelerates in a non-linear fashion, causing the option to lose value rapidly with each passing day, even without relevant movements in the underlying. The roll over avoids this inefficient phase and allows the time value to be preserved by moving the position to a more distant maturity where the time attrition is again lower and more manageable.
Renewal discipline
The roll is executed systematically, closing the current call and opening a new ATM contract with a maturity of 90-120 days. This process maintains consistency in the strategy, avoids the inefficient acceleration phase of the theta-decay and preserves the largest convexity of at-the-money contracts in optimal time ranges.
Profitability objective
Each cycle seeks a return of close to ~100% on the initial premium. The convexity of ATM calls allows capturing profits disproportionate to the cost, keeping the risk limited to the initial cost and avoiding entering into inefficient phases of theta-decay through systematic management of the roll.
Hedging function
The use of calls instead of direct exposure in equities allows maintaining a bullish bias with a controlled maximum loss (premium). The strategy provides flexibility to adjust maturities and strikes according to market evolution, acting as a tactical hedge against corrections.
Application in ETFs
In my case, I run this strategy on Liquid and leveraged ETFs linked to major benchmark indicessuch as SPY, QQQ, SPXL or TECL in the US market. These vehicles accurately replicate the performance of the main indexes (SPX and NDX) and offer several operational advantages:
- Liquidity and tight spreadswhich allow entering and exiting positions with low transaction costs.
- Depth in the options chainwith well-distributed strikes and regular maturities, which facilitates the execution of roll overs in a systematic manner.
- Diversified exposureThe company's portfolio is composed of broad baskets of securities, reducing the idiosyncratic risk inherent to individual stocks.
- Efficient risk managementThe ETF structure allows adjusting the size of the position and maintaining direct correlation with the indexes most followed by the institutional flow.
Thus, applying this strategy in ETFs not only maintains the logic of convexity and control of theta, but also provides greater operational efficiency and consistency in the replication of the sought-after upward bias.


